Understanding recursion

Recursion - how to not get overwhelmed

I am sure that throughout your programming journey you have encountered recursive functions. It is one of the more challenging concepts in programming for budding software engineers to grasp. Even though one might rarely encounter recursion in their day-to-day work, it is a crucial concept in the realm of computer science. So I have written this post and hope that it will help you understand this topic better.

We should start from the very beginning. What is recursion?

Recursion is the process of a function calling itself. You can think about it as some sort of a loop. As you might already know, every loop has to have a condition to stop calling itself. It is the same in case of recursive functions, the condition stopping the loop is called base case. If you forget about specifying the base case, the loop will run indefinitely and you will encounter stack overflow.

When should you use it?

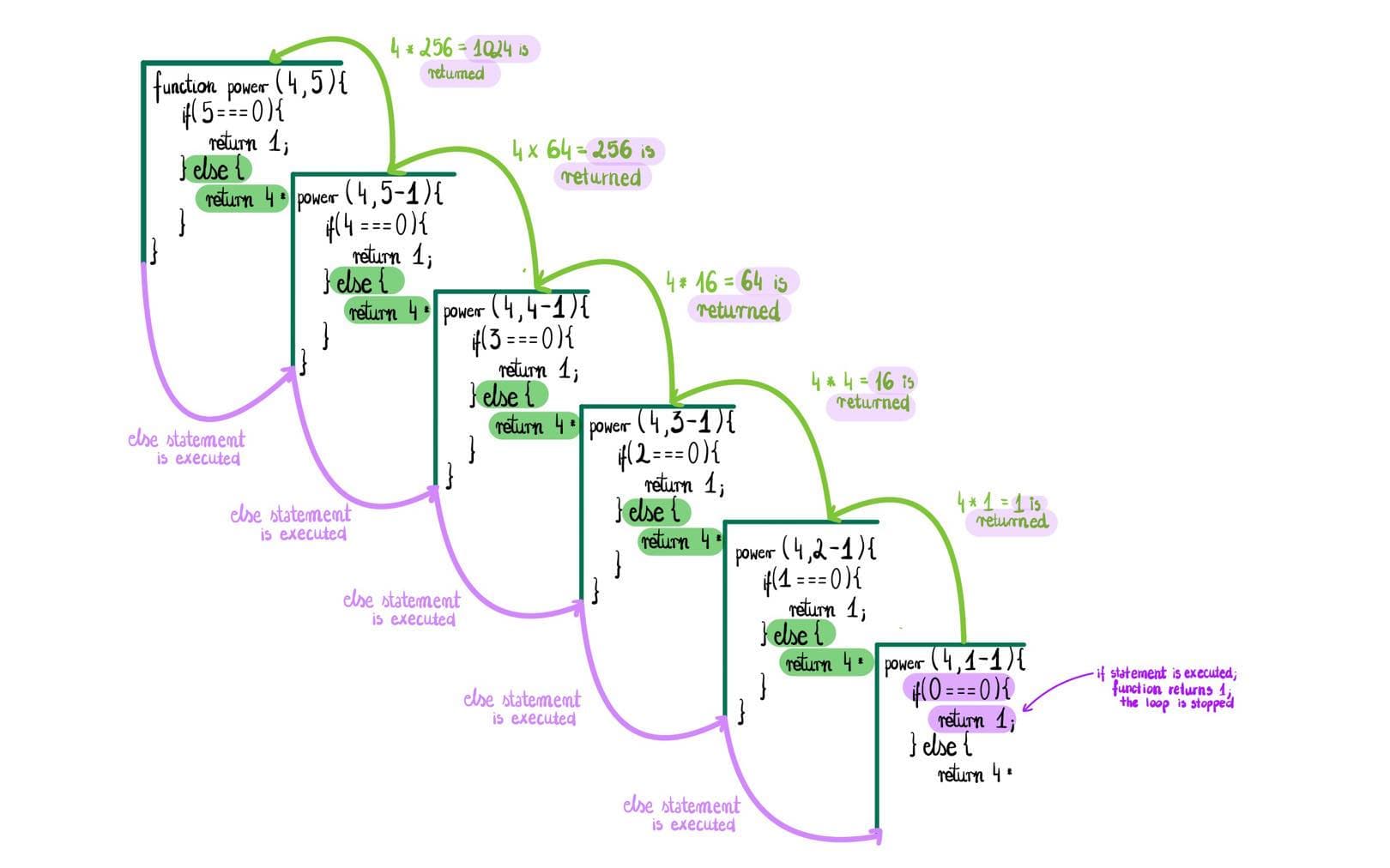
You could use recursion when you have a problem which can be divided into smaller, repetitive subproblems. A great example of this kind of problem is writing a function which will raise a given base to the power of a given exponent.

// FUNCTION POWER
 
  function power(base, exponent){
 
    //base case, loops stops and returns one.
    if(exponent === 0){
    	return 1;
    } else {
    //if exponent is not 0, multiply the base by the base
      return base * power(base, exponent - 1)
    }
  }
console.log(power 4, 5)
=====> 1024

Graph visualising the recursion process

//CHECKING IF THE NUMBER IS ODD
//you can check whether the number is even or odd
//by simply subtracting the number two from the number,
//if what’s left is 0 - the number is even, otherwise it is odd
 
function isEven(n) {
  //in this example we are having two base cases
  if (n === 0) return true;
  if (n === 1) return false;
 
  //this line is covering for negative numbers,
  //otherwise you would end up with infinite function again
  if (n < 0) return isEven(-n);
  //if the number is not equal 0 || 1 then subtract
  //number two from the “n” number
  else return isEven(n - 2);
}

What is the time complexity of the recursive function?

For one-branch recursion the time complexity will be the big O(n). It is due to the fact that to compute the result we would have to go through n steps.

The space complexity would also equal to the big O(n) as we are invoking this function n times and every function takes space in the memory.

This space complexity is very inefficient, recursive function implementations in JavaScript are also typically three times slower than loops.

Why would we use it then?

I think it is due to the fact that some problems are easier and more elegant to solve with recursion than loops.

If you don’t understand it yet, it is okay. Understanding and implementing recursion takes time, so take yours🙂

Have fun with your future programming endeavors!

E.N.